from Lagash Astarte Ritual Sumerian Studies Spring Equinox 2001

Musical Theory and Ancient Cosmology by Ernest G. McClain

In ancient Mesopotamia (Sumer, Sumner), music, mathematics, art, science, religion, and poetic fantasy were fused. Around 3000 B.C., the Sumerians simultaneously developed cuneiform writing, in which they recorded their pantheon, and a base-60 number system. Their gods were assigned numbers that encoded the primary ratios of music, with the gods’ functions corresponding to their numbers in acoustical theory. Thus the Sumerians created an extensive tonal/arithmetical model for the cosmos. In this far-reaching allegory, the physical world is known by analogy, and the gods give divinity not only to natural forces but also to a “supernatural,” intuitive understanding of mathematical patterns and psychological forces.

The cuneiform mathematical notation, invented by Sumer, was fully exploited by the virtuoso arithmetical calculations of Babylon, politically ascendant in the second millennium. The notation employs few symbols, which are distributed in patterns easily understood by the eye. Thus, few demands are made on memory. In Mesopotamia, mythology took concrete form; for example, important activities of the gods can be read as “events” in a multiplication table notated as a matrix of Sumerian bricks. Classical Greece abstracted all of the rational tonal concepts embedded in this Sumerian/Babylonian allegory for two thousand years, simply waiting to be demythologized. Moreover, because the religious mythologies of India, China, Babylon, Greece, Israel, and Europe use Sumerian sources and numerology, theology needs to be studied from a musicological perspective.

If science is conceived of as knowledge and philosophy as love of wisdom, then the invention of musical theory clearly is one of the greatest scientific and philosophical achievements of the ancient world. When, where, and how did it happen?

Assuming that Cro-Magnon man processed sound with the same biology we possess, humans have shared some fifty thousand years of similar auditory experiences. Musical theory as an acoustical science begins with the definition of intervals, the distance between pitches, by ratios of integers, or counting numbers, a discovery traditionally credited to Pythagoras in the sixth century B.C.

Not until the sixteenth century A.D., when Vincenzo Galilei (Galileo’s father, an accomplished musician) tried to repeat some of the experiments attributed to Pythagoras, was it learned that they were apocryphal, giving either the wrong answers or none at all. Today, as the gift of modern archaeological and linguistic studies, our awareness of cultures much older than that of Greece has been phenomenally increased; this permits us to set aside the tired inventions about Pythagoras and tell a more likely story, involving anonymous heroes in other lands.

Cuneiform, considered the world’s first writing,
developed among the merchants of Sumer.
A triangular stylus was pressed into hand-sized slabs of wet clay,
then the clay was baked.
Most cuneiform tablets record commercial transactions.

What seems most astounding in ancient Mesopotamia is the total fusion of what we separate into subjects: music, mathematics, art, science, religion, and poetic fantasy. Such a fusion has never been equaled except by Plato, who inherited its forms. Socrates’ statement about the general principles of scientific studies in book 7 of Plato’s Republic, with the harmonical allegories that follow directly in books 8 and 9, guides my exposition here. The Mesopotamian prototypes to which they lead us fully justify Socrates’ treatment of his own tale as an “ancient Muses’ jest,” inherited from a glorious, lost civilization. Scholars who have become too unmusical to understand mankind’s share in divinity, as Plato feared might happen, still can lean on him for understanding, for all of his many writings about harmonics and music have survived. (I must suppress here, for reasons of space, the extensive harmonical allegories of the Jews, whose parallel forms infuse the Bible with related musical implication from the first page of Genesis to the last page of Revelation.)

Music was as important in ancient India, Egypt, and China as it was in Mesopotamia and Greece. All these cultures had similar mythic imagery emphasizing the same numbers, which are so important in defining musical intervals; this raises doubts about whether any people ever “invented” acoustical theory. For instance, in any culture that knows the harp as intimately as it was known in Egypt and Mesopotamia, its visible variety of string lengths and economy of materials (strings require careful and often onerous preparation) encourage builders, as a sheer survival strategy, to notice the correlation between a string’s length and its intended pitch.

Similarly, in China, where by 5000 B.C. the leg bones of large birds, equipped with tone holes appropriate for a scale, appear as paired flutes in ritual burials, the importance of suitable materials conditioned pipemakers to be alert to lengths. The basic ratios could have been discovered many times in many places, more likely by loving craftsmen and practitioners than by philosophers. Certainly, the discovery came no later than the fourth millennium B.C., before even the first Egyptian dynasty was founded or the Greeks had reached the Mediterranean shore.

A NEWLY EMERGING PERSPECTIVE.
In the fourth millennium B.C., the Sumerians, a non-Semitic people of uncertain origin, developed a high civilization in Mesopotamia, now the southern part of Iraq. For reasons that have been vigorously argued but remain unclear, they developed a base-60 number system. Waiting to be recognized within it–and in ways obvious to any scribal adept, although invisible to the illiterate–were the main patterns of harmonical theory that appear later in India, Babylon, and Greece. Sumerian tombs of this early period yield a harvest of harps, lyres, and pipes, and the literature surviving on clay tablets abounds in elaborate hymns.

In the cuneiform writing of the Sumerians, which was invented concurrently with the base-60 number system, the pantheon of deities is rationalized by assigning to the high gods the base-60 numbers that, as we shall see, encode the primary ratios of music. The glyph, or symbol, for heaven or star, followed by the appropriate number, functions as a “god nickname.” (The numerical values of the deities are given in Budge 1992.) The numbers reveal their significance in triangular arrays of pebble counters.

Furthermore, in the mythology of their religion, the responsibilities and behavior of the gods correspond with the functions of the god numbers in base-60 acoustics. Sumerian cosmology is grounded in the metaphorical copulation of the male A and female V numerical arrays, from which the Greek “holy tetraktys” is abstracted.

For example, the head of the pantheon and father of the gods is the sky god An (the thanAnu), god 60, written in cuneiform as an oversize 1 sign. Because base-60 numbers enjoy potentially endless place value meanings as multiples or submultiples of 60 (like the unit, 1, in decimal arithmetic), An = 60 (written as 1) functions as the center of the whole field of rational numbers. In mathematical language, An is its geometric mean, being the mean between any number and its reciprocal.

Anu/An, therefore, is essentially a do-nothing deity, as he was later accused of being-, a reference point, perfectly suited to represent simultaneously the middle band of the sky, the center of the number field, and the middle, reference tone (the Greek mese) in a tuning system. He was fated to be deposed by more active leaders among his children, as harmonical logic focused more clearly on structure and sheer virtuosity in computation became subordinated to deeper mathematical insight.

Theology, from its birth as “rational discourse about the gods” and in many later cultures influenced by Sumer, is mathematical allegory with a deeply musical logic. Tuning theory today remains a fossil science with no change at all in its basic parameters–structured by the gods themselves in numerical guise–since it premiered in Sumer about 3300 B.C.

To glimpse this new vision requires that we lay aside our algebra, our computers, and our pride in rational superiority and represent numbers to ourselves as the ancients did: concretely. We must learn to do musical arithmetic with a handful of pebbles in a triangular matrix, as the Pythagoreans teach us, imitating the pattern of bricks in the Sumerian glyph for mountain.

Then, like Socrates, we must show ourselves the harmonical implications of that arithmetic with a circle in the sand, for that circle is the cosmos, viewed as endlessly cyclical, like the tones of the musical scale.

In what follows I am presenting Mesopotamian arithmetic as Plato still practiced it in the fourth century B.C., studying his mathematical allegories for clues to earlier examples. Plato is the last great harmonical mythographer of the European world; never again did a major philosopher so thoroughly ground his thinking in music.

In retrospect, decoding Sumerian-Platonic harmonics proves astonishingly simple. Anyone, even a child, who can count to ten and sing or play the scale can make self-evident the scale constructions that once modeled the cosmos.

Because 60 is integrally divisible by 2, 3, 4, 5, 6, 10, 12, 15, 20 and 30, base-60 arithmetic can correlate many subsystems, allowing fluent manipulation of fractions. This very early mastery of fractions ensured adequate arithmetical definition of pitch ratios–presumably as string-length ratios on early harps, approximate length ratios on the flutelike panpipes, or tone-hole ratios on the aulos–no matter how many tones are involved and whether pitch patterns rise or fall.

About 1800 B.C., the Babylonians became politically ascendant and reorganized the Sumerian pantheon, keeping its god numbers and related mathematical terminology. They developed base- 60 computation to a level of arithmetical virtuosity not equaled in Europe until about A.D. 1600 and not understood in modern times until the middle of our own century (see Neugebauer 1957). Not until 1945, when Neugebauer and A. Sachs published the translation of cuneiform tablet YBC 7289 from the Yale collection, did the world learn that ancient Babylon (1800-1600 B.C.) possessed a base-60 formula for the square root of 2 accurate to five decimal places (1.41421+), or the formula for generating all Pythagorean triples (a triangle with sides of 3, 4, and 5 units is merely an example) a thousand years before Pythagoras explicated the first one.

The Greeks, still thinking in terms of Egyptian unit fractions (so that a descending whole tone of 8:9, for instance, was constructed by laboriously adding to the reference length 1/8 of itself), would have been astonished to learn that the Egyptians, whom they revered, had like themselves been far surpassed in computational facility by an ancient neighbor.

The paucity of surviving Sumerian mathematical texts requires scholars to make many inferences from later Babylonian survivals, and much Sumerian literature remains untranslated or inaccessible. Thus, as further linguistic evidence becomes available, the story I tell here will require revision, becoming more certain in dating, clearer in meaning, and richer in detail.

To look ahead in history and see the persistence of Sumerian/Babylonian methods, Ptolemy, in the second century A.D., in the Harmonica, recorded all of the some twenty Greek tunings known to him with sexagesimal (base-60) fractions. Between about 500 B.C. and A.D. 150, Babylonian and Greek astronomy thrived on base-60 computation. It was still used by Copernicus in the fifteenth century and endures in modern astronomy. The Chinese calendaris still reckoned by 60s. Astronomy, however, as the science of precise measurement that it later became, “was practically unknown in ancient Sumer; at least as of today we have only a list of about twenty-five stars and nothing more” (Kramer 1963).

HOW BASE-60 SURVIVES IN TIME MEASUREMENT
Analog clocks and watches equipped with rotating hands for hours, minutes, and seconds are living fossils of the Sumerian arithmetical mind-set.

a. Numbers have visible and tangible markers on the dial (representing the fixity of the recurring temporal cycle), restricting burdens on memory and permitting operations to be reduced to counting and adding.

b. Sixty can be conceived of, when we please, as a large unit (one rotation of the second or minute hand), conversely giving the small unit the implication of 1/60.

c. The large unit, alternately, can be conceived of as a higher power of 60 (correlating the simultaneous rotations of both second and minute hands), for 60 X 60 = 3,600 seconds is also one hour, conversely giving our small unit the implication of 1/3,600.

d. Twelve hours constitutes a still larger unit (one rotation of the hour hand) of 12 x 60= 720 minutes, and 12 x 3,600 = 43,200 seconds, conversely giving the smallest unit the implication of 1/720 or 1/43,200.

e. We avoid confusion between these alternate arithmetical meanings the same way the Sumerians did, namely, by remembering the context of the questions we are trying to answer.

f. The existence of alternative ways of expressing a unit, as in the examples above, indicates and emphasizes the importance of reciprocals.

Musicians, following Plato, still project their tones into a circle that eliminates cyclic octave repetitions (Plato, in the Timaeus, insists that God makes only one model of anything). Thus today, using our modern, equal-tempered scale, we can identify any musical interval as some multiple of a standard semitone, to the envy of calendar makers, who, having to deal with the irregularities of days, months, and years, are jealous of our perfect twelve-tone symmetry. But the nearest approximation of our twelve-tone, equal-tempered scale in small integers remains that provided by ancient base-60 arithmetic.

SUMERIAN NUMBERS
Sumerian numbers were impressed on small clay tablets with a stylus, at first round,later triangular, held slanted for some numbers and vertically for others. Numbers from 2 to 9 were built up by repetitions of the unit, made with the edge of the stylus. A 10 was imprinted with the end; a 60 was made as a large 1 by pressing the stylus more firmly into the clay. The equation 60 X 60 = 3,600 was scratched in as a circle (see vander Waerden 1963). Only a few symbols were needed, and repetition made them easy to decode, minimizing burdens on memory. The idea of a number was actually embodied in the strokes required to notate it.
Computation was made easy by tables of “reciprocals, multiplications, squares and square roots, cubes and cube roots, …exponential functions, coefficients giving numbers for practical computation,…and numerous metrological calculations giving areas of rectangles, circles” (Kramer 1963). Many copies of these tables have come down to us.

The standard multiplication tables pair each number with its reciprocal and give special prominence to the favored subset of “regular” numbers, whose prime factors are limited to 2, 3, and 5 (larger prime factors necessarily lead to approximations in the reciprocals). “Regular numbers” up to 60 are shown with their reciprocals, transcribed, for instance, so that the reciprocal of 40/60 = 2/3 reads 1,30, meaning 90/60 = 3/2. Notice that only the most important fractions of 60 are deified (1/6, 1/5, 1/4, 1/3, 1/2, 2/3, and 5/6). The tone names are nearest equivalents in modern notation. Several values require three sexagesimal “places” (indicated by commas); auxiliary tables freely employ six, seven, and even more places.

SUMERIAN SYMMETRY OF OPPOSITES

A telling clue to the psyche–of Sumerians, of Plato, and of ourselves–is affection for the symmetry of opposites. Inverse, or bilateral, symmetry conditions base-60 computation, as it conditioned Platonic dialectics. (“Some things are provocative of thought and some are not…Provocative things…impinge upon the senses together with their opposites.” Republic 524d) When facing a mirror we exhibit to ourselves, with varying degrees of perfection, this symmetry of left/right opposites across an imaginary “plane of reflection.”
The old-fashioned scale, or balance beam, epitomizes this notion. The balance owes its functioning to gravity, but its appeal to us, its attractiveness, is due to our ear, which in addition to being the organ of hearing is also the personal organ of balance. Our empathic human feelings for the balance beam affect the inverse, orbilateral, physical symmetry because of the experience of balancing our own bodies, an activity dependent on the ear, not the eye. All of the computations presented later will be aligned in this basic symmetry, with Anu/An = 60 (meaning 1) on the balance point. Sumerian art greatly elaborates this symmetry of opposites.

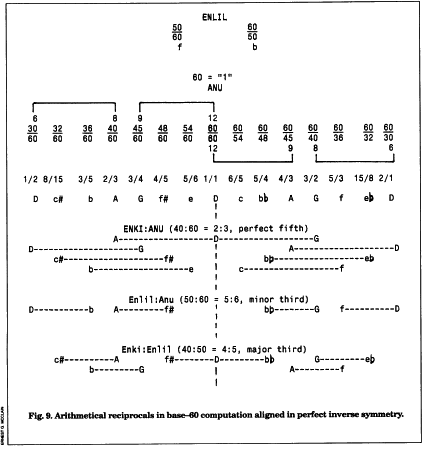
THE DEIFICATION OF TONE NUMBERS

The deified Sumerian numbers, taken over by Babylon, are 10, 12, 15, 20, 30, 40, and 50, all fractional parts of “father” Anu/An = 60, head of the pantheon. Their fractional values and god names are indicated here with a brief description of their mythological functions.

Anu/An, 60, written as a large 1, “father of the gods” and earliest head of the pantheon, is any reference unit. He is equivalent in our notation to 60/60 = 1, where he functions, according to modern concepts, as “geometric mean in the field of rational numbers.”

Enlil, 50 (5/6), “god on the mountain” possessing fifty names, is mankind’s special guardian and was promoted to head the pantheon circa 2500 B.C. Enlil deities in base 60 what the Greeks knew as the human prime number, 5, in their base-1O harmonics. By generating major thirds of 4:5 and minor thirds of 5:6, he saved Sumerians tremendous arithmetical labor, as we shall note in due course.

Ea/Enki, 40 (2/3), “god of the sweet waters” and perhaps the busiest deity in Sumer, “organizes the earth,” including the musical scale. He deities the divine prime number, 3, in the ratio of the musical fifth 2:3, the most powerful shaping force in music after the octave. (Notice that the trio of highest gods (40, 50, 60) defines the basic musical triad of 4:5:6 (do, mi, sol, rising, and mi, do, la, falling). The ratio 4:5 defines a major third and the ratio 5:6 defines a minor third, taken either upward ordownward within the matrix of the musical octave.)

Sin, 30 (1/2), the Moon, establishes the basic Sumerian octave matrix as 1:2 30:60.

Shamash, 20 (1/3), the Sun, judges the gods.

Ishtar, 15 (1/4), is the epitome of the feminine as virgin, wife, and everybody’s mistress.

Nergal, 12 (1/5), is god of the underworld.

Bel/Marduk, 10 (1/6), the biblical Baal, originally was a minor deity but eventually became head of the Babylonian pantheon in the second millennium B.C. He inherited all the powers of the other gods, including Enlil’s fifty names, in a giant step toward a”Pythagorized” monotheism built on the first ten numbers.

GREEK HARMONICAL PRINCIPLES IN SUMERIAN ARITHMETIC

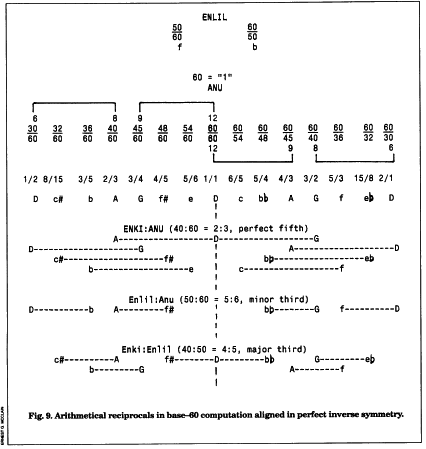
Here are the principal arithmetical symmetries of base-60 Sumerian harmonics, summarized in the inverse “heraldic” symmetry displayed above but expressed as modern fractions. Every tone in the scale will be found to participate in numerous god ratios,and all other ratios are their derivatives via multiplication (which is what Plato means by “marriage” in his elaborate metaphor in the Republic). All of the harmonical concepts in my analysis, however, are Greek. Plato’s formula for this particular construction can be found in the Republic, book 8; his discussion of general harmonical principles is in the Timaeus.
All pitch classes generated by the prime numbers 2, 3, and 5, up to the index of 60, are represented here (fig. 9). Remember that all doubles are equivalent, so that 3, 6, 12,and 24 define the same pitch as 48, for example.

a. Tones are defined by numbers.

b. The significance of a number lies only in its ratio with other numbers.

c. Numerosity is governed by strict arithmetic economy. Because Sumerian double meanings were assumed, the numbers 30, 32, 36,… are in smallest integers for this context. This economy is obscured somewhat by writing ratios as fractions; mentally eliminate the superfluous reference 60s.

d. Every number is employed in two senses, as great and small, displayed here as reciprocal fractions.

e. The double meanings of great and small require the basic model octave to be extended across a double octave from 30/60 = 1/2 to 60/30 = 2.

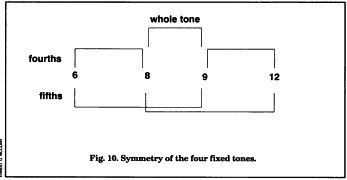
f. Tones are grouped by tetrachords (that is, in groups of fours) whose fixed boundaries always show the musical proportion 6:8 = 9:12, defining the octave (6:12 = 1:2), the fifth (2:3, that is, 6:9 and 8:12), and the fourth (3:4 or 6:8 and 9:12).

Notice how the arithmetic mean 9 and the harmonic mean 8 establish perfect inverse symmetry and define the standard whole tone as 8:9. These ratios define the only fixed tones in Pythagorean tuning theory, and they are invariant. Pythagoras reputedly and plausibly brought this proportion home from Babylon in the sixth century B.C. In base 60, these “framing” numbers necessarily are multiplied by 5 into 30:40 = 45:60.
Notice that Ea/Enki, god 40, defines these frames (D:A falling and G:D rising) in his double role as 40:60 and 60:40 and thus literally “organizes the earth” (as represented by the string) into do, fa, sol, do, harmonic foundations of the modern scale.

g. The Enlil = 50 tones of pitch classes b and f always belong to the opposite scale, for the god shares these tones with 36 (that is, 30:36 = 50:60 and 30 and 60, “beginning and end,” coincide); thus, Enlil is free to supervise the system by reminding us of the symmetry of opposites.

Enlil’s promotion to head the pantheon possibly symbolizes this insight. He plays a very active role, also generating several intervals that actually reduce numerosity, whereas the primal procreator, Anu/An = 60, a do-nothing deity of little account in Sumer and Babylon, remains purely passive.

Platonic dialectics, however, emphasize anew the importance of an invariant t4 seat in the mean,” thus turning Anu/An’s passiveness as geometric mean into the greatest possible Socratic virtue as “the One Itself.”

h. The falling or descending version of this scale, as notated is in our own familiar major mode. It is more commonly notated one tone lower, on the white keys of the C octave. The rising scale on the right, its symmetric opposite, is the basic scale of ancient Greece, India, and Babylon. It is more simply notated one tone higher, on the white keys in the E octave.

My choice of D as reference pitch is dictated by the necessity of showing opposites simultaneously, in the Sumerian normative arithmetical habit that Plato later required of his students in dialectic. Future philosopher-guardians in idealized cities needed to become expert in weighing the merits of contradictory claims, requiring the ability to see opposites simultaneously. Music provided the opportunity to do this, par excellence, and so childhood training began with it.

AN OVERVIEW OF CALENDAR AND SCALE
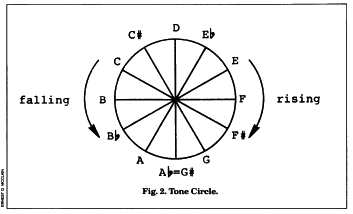
To coalesce the musical opposites shown above into one Sumerian/Platonic overview, eliminating all octave replication and laying bare the irreducible structure (“God’s only model”), we need only project these tones into the same tone circle.

From Plato’s mythology (in the Critias) come “Poseidon and his five pairs of twin sons”, aligned in perfect inverse Sumerian symmetry across the central vertical plane of reflection. (Poseidon, at twelve o’clock, Greek successor to the water god Ea/Enki, is self-symmetric, being both beginning and end of the octave no matter whether we traverse it upward or downward.) These eleven tones constitute the only pitch class symmetries up to an index of 60.

But to coalesce opposite fractions so that the numbers–like the tones–show the same ratios when read in either direction, we must expand the numerical double 1:2 into 360:720. If we confine ourselves to three-digit numbers, there is, in addition to Poseidon’s ten sons, only one other pair of symmetric numbers, namely, 405 and 640 (since 405:720 = 360:640). These are notated here as C and E to indicate their very slight and melodically insignificant difference from c and e. This microtonal “comma” difference of 80:81, barely perceptible in the laboratory and then only by a good ear, was taken by the Greeks as the smallest theoretically useful unit of pitch measure and is approximately 1/9 of their standard whole tone of 8:9. The whole-tone interval between A and G invites similar subdivision, and symmetry requires a point directly opposite our reference, D. This locus is defined by the square root of 2, lying beyond the ancient concept of number, and so we must search for an approximation.
A musically acceptable candidate (its error is actually less than a comma) now appears at a-flat = 512, or, alternately, g-sharp = 512, only slightly askew our ideal value and with the “god ratio” of 4:5 with C or E.

Plato’s Poseidon and his ten sons are shown again, together with the new symmetry pair C/E and the alternate a-flat/g-sharp pair (one of which is always missing in the 360:720 octave). My vertical pendulum now swings gently back and forth to either side of six o’clock as the numbers are read alternately in rising and falling scale order (that is, as great and small).

At 512, where a-flat is not quite equivalent to g-sharp, the ancients had little choice but to accept this arithmetical compromise with perfect inverse symmetry.

How did they rationalize such a complicated, inverse symmetry, one ultimately defeated because of the compromise? Remembering the quite ancient correlations of scale and calendar, let us apply imagination to their problem.

This base-60 model can be imagined as an appropriate correlate to the lunar calendar of Sumer and Babylon, as it later became the map of an idealized circular city in Plato’s Laws, calendar and musical scale being assumed to have a similar cosmogony. Notice the following correspondences:

a. The basic seven-tone scale requires the thirty digits in the 30:60 octave, and 30 is deified as Sin, the Moon, and the basic octave limit.

b. The two opposite seven-tone scales and the symmetrically divided tone circle correspond with Sumer’s two agricultural seasons, in which irrigation during the dry summer complemented the rainy winter harvest.

c. In the octave double between 360 and 720, which coalesces opposites, there are 360 units to correspond with the schematic calendar count of 12 x 30 = 360 days. (Eventually, astronomers in India and Babylon defined these units as tithis, meaning 1/360 of a mean lunar year of 354 days, hence slightly less than a solar day. Greek astronomers eventually defined the same 360 units geometrically as degrees. Neither development is relevant to ancient Sumer.)

d. Tonally acceptable but acoustically inaccurate semitones, alternately small (24:25) and large (15:16), correspond with the lunar months embodied in ritual, alternating between 29 and 30 days.

e. Between a-flat = 512 and g-sharp 512 (in the opposite sense), a gap corresponds with the excess of a solar year over 360 and the defect of a lunar year of 354 days from 360.(Five and a quarter extra solar days are about a 1/69 of 360, while the gap in the reduced comma is actually about 1/60 of an octave, a remarkable near-correspondence.)

Because any successful agricultural society must find some way to accommodate lunar, solar, ritual, and schematic cycles with the growing cycle, we need not suppose that Sumerians or anyone else ever really believed the year contained 360 days. Only a musicology dedicated to numerical precision and economy finds 720 days and nights (that is, 360 days and 360 nights) cosmogonically correct.

All of the tonal, arithmetical, and calendrical relations discussed above are coincidences. They exist among base-60 numbers whether or not anyone is aware of them, mainly because 60 is divisible by three prime numbers, 2, 3, and 5, and no others, and 60 is being used in the way we use a floating-point decimal system.

If Sumerian mythology did not offer persuasive evidence that Sumerians were conscious of tonal implications, then their establishment of a base-60 system, which included such perfect models for a lunar-oriented culture and for Pythagorean harmonics two thousand years later, would be pure serendipity, meaning that it resulted from “the gift of finding valuable or agreeable things not sought for.” But the most interesting evidence for Sumerian harmonical self-consciousness is yet to be shown via Plato’s kind of triangular matrices, functioning as “mothers” in harmonical arithmetic.

In Plato’s Greece, the harmonical wisdom of Babylon and India was transformed into political theory. Men now acted out the roles once assigned to gods. Plato’s four model cities–Callipolis (in the Republic), Ancient Athens and Atlantis (both in the Critias),and Magnesia (in the Laws)–were each associated with a specific musical-mathematical model, all generated from the first ten integers. All are reducible to a study of four primes: 2, 3, 5, and 7.

In the Republic and Laws, idealized citizens–represented as number–generate only in the prime of life. For Plato, this means that 2 never really generates anything beyond the model octave 1:2, for this “virgin, female” even number–with all of its higher powers–designates the same pitch class as any reference 1.(Multiplication by 4, 8, 16,… generates only cyclic identities, different octaves of tones we already possess. They are Plato’s “nursemaids,” carrying tone children until they are old enough to “walk” as integers; hence, as he says, his “nurses” require exceptional physical strength.)

The multiplication table for the 3 x 5 male odd numbers, however, generates endless spirals of musical fifths (or fourths) and thirds; within the female octave 1:2, new pitches are generated at the same invariant ratios. The Greek meaning of symmetry is to be in the same proportion. Thus, a continued geometric proportion (like 1, 3, 9,27,…or 1, 5, 25,…) constitutes “the world’s best bonds,” maximizing symmetry, which is obscured by mere appearances when these values are doubled to put them into some preferred scale order. The multiplication table for 3 x 5 graphs multiple sets of geometric tonal symmetries (Plato’s only reality) as far as imagination pleases.

Greece inherited its arithmetical habits from Egypt, including an affection for unit fractions in defining tunings (the ratio 9:8 was thought of as “eight plus one-eighth of itself,” and so on). It awoke to number theory only when it became acquainted with Mesopotamian methods. Thus, the travels of Pythagoras, whether legendary or not, played an important role. Those methods apparently were new enough in Plato’s fourth century B.C. to invite his extensive commentary, yet old enough so any novelty on Plato’s part was absolutely denied by Aristoxenus (fl. circa 330 B.C.) within fifty years.

Plato is responsible for an astonishing musical generalization of the base-60 tuning formula as 4:3 mated with the 5. His 3, 4, and 5 correspond with Sin = 30, Ea = 40, and Enlil = 50 and remind us that all tones are linked by perfect fourths, 4:3, which define possible tetrachord frames, or by perfect thirds, 4:5. The last Pythagorean who really understood Platonic “marriages” may have been Nicomachus in the second century A.D.; he promised an exposition but none survives.

BABYLONIAN REORGANIZATION OF THE PANTHEON

In the second millennium B.C., the Babylonians reorganized the inherited Sumerian pantheonin a way that very strongly points toward its Pythagorean future. To avoid destruction by Enlil, who is disturbed by their confusion and noise, the gods reorganize under the leadership of Marduk, god 10, the biblical Baal, to whom all the other gods cede their powers.

Herein lies a beautiful reduction of Sumerian expertise with reciprocal fractions to a more philosophical overview of harmonics as being generated exclusively by the first ten integers (Socrates’ “children up to ten,” in the Republic, beyond which age he doubted citizens were really fitted for ideal communities).

To celebrate their survival after Marduk defeats the female serpent Tiamat, sent to destroy them, the gods decree him a temple; the bricks require two years (2 x 360 = 720) to fabricate. This mythologizes 720, the Sumerian unit of brick measure, and the smallest tonal index able to correlate seven-tone opposites into a twelve-tone calendrical octave. When Marduk’s tonal/arithmetical bricks are aligned in matrix order, we see that the general shape of his temple (with an index of 720) is an enlarged form of Enlil’s temple (with an index of 60); Enlil now confers his fifty names on Marduk. This temple makes Marduk’s face shine with pleasure, we are told.

Let me conclude our discussion of Marduk’s victory over the dragon, Tiamat.

‘GREAT DRAGON’ TUNING
It is now a normal part of a child’s musical education to learn to view the scale as a spiral of musical fifths and fourths, as they are actually tuned–for the convenience of the ear–and to be shown those tones in a tone circle. That up-and-down, alternating cycle of pitches inspires, I propose, the dragon and great serpent lore of ancient mythology.

Serpentine undulations are visible to any harpist in the lengths of successive strings when taken in tuning order (as they still necessarily are), and the undulations can be seen in any set of pitch pipes when similarly aligned, as in China. Because the same tone numbers function reciprocally as multiples of frequency and of wavelength, they have the same double meanings today that they enjoyed in Sumerian times. It is entirely appropriate, therefore, to represent this spiral both forward and backward, simultaneously, with intertwined serpents.

In the mythological account, Marduk slays the dragon (which is presumably the continuum of possible pitches represented by the undivided string) by first cutting it in half to establish the octave 1:2. Further cutting presumably “sections” the other pitches. No numbers larger than Marduk’s–meaning 10–play any role in geometrical sectioning of the string.

This “serpentine” double meaning–rising and falling musical fifths and fourths–lies at the very heart of our consciousness of musical structure. Sumer did not hesitate to make the double serpent the center of symmetry, as on this steatite vase of Gudea, priest-king of Lagash circa 2450 B.C., where they are flanked symmetrically by gryphons.
Large and unwieldy numbers can be avoided if the 4:5 and 5:6 ratios introduced by Enlil are used to define the seven-tone scale (in which case all the numbers are of two digits). Used for the twelve-tone scale, his numbers need only three digits. Thus, in Sumer, Enlil= 50, base-60 deification of the human, male prime number 5, grossly reduces our computational labors from six-digit Pythagorean numerosity (in which a twelfth tone requires 311 = 177,147) to no more than three, and without noticeably diminishing melodic usefulness. Only the five central tones (CGDAE) from the Great Serpent appear. All other tones are owed to Enlil.
Historically, European music reintroduced this Just tuning system in the fifteenth century A.D. to secure perfect 4:5:6 triads for its new harmonies without exceeding twelve tones. The ancients probably loved it more for its arithmetical economy than for its triadic purity. Microtonalists today, equipped with a powerful new technology, are again searching for an effective employment of these ancient Sumerian god ratios.

The ultimate origins of music theory, as opposed to the Sumerian codification that I deduce here, remain lost in the far more distant past, like the origin of our sense for number. They are grounded in a common aural biological heritage, some of which we share with other animals, and are by no means dependent, as Aristotle noted, on precise numerical definition. As eminent contemporary musicologist William Thompson explained in our correspondence,

In adapting to our complex environment, our sensory ingestive systems have become…forgiving filters, enabling us to generalize….This, I’m convinced, is a product of very early adaptive behavior, a part of our survival good fortune…in that our neural system has developed myriads of networks which are overachievers when it comes to doing some simple jobs.

Socrates never believed in the possibility of perfect justice. The great aim of Plato’s Republic was to help readers become more “forgiving filters” for alternative cultural norms. There remains a certain fuzziness about a scientific definition of musical intervals, as there is about the Republic’s days and nights and months and years, and art has turned that into something for which we all can be grateful. Sumerian “overachievers”–and these “black-headed people,” as they called themselves, proved historically to be as aggressive as the great heroes they knew or invented–achieved a tremendous synthesis of cultural values. They challenge us to do as well.

https://ancientmystery.info/Music-Sumer-McClain.htm

https://sites.google.com/site/432octaves/cuneiform-tablets

https://sites.google.com/site/432octaves/sumerian-cyclical-tuning-system

 Studio Vision Pro 3.0.6 [k].sit (34.72 kB – downloaded 149 times.)
 SVPro3.0.6Update.sea.hqx (2700.65 kB – downloaded 130 times.)
 StudioVisionPro 3.0.2.sit (1366.35 kB – downloaded 134 times.)

Studio Vision Pro is professional digital audio recording and MIDI sequencing software that gives you the ability to display and manipulate information in a myriad of musically meaningful ways. It makes technology transparent–letting you work intuitively, and fostering your creativity.

Studio Vision Pro is a comprehensive, integrated suite of software, with a diversity of abilities that defy the boundaries of what we can show you on a web page.

As incredible as it sounds, Studio Vision Pro 3.0 really does let you edit digital audio as if it were a MIDI sequence. It also lets you map digital audio to MIDI–so that the audio follows MIDI beautifully, expressively, and musically.

What follows is a brief overview. To truly understand the depth and power of Studio Vision Pro, you’ll just have to put it to work on your next project.

Track Overview
The Track Overview is a “global information center” for your MIDI and audio tracks and provides a wealth of user feedback and control. Track Overview lets you see the contours of your music by faithfully representing audio waveforms as well as MIDI data.

Alternately, tracks can be viewed in Block Mode, which allows you to size blocks instantly in sections as small as an 8th note, or as large as 16 bars. Tracks Mode displays tracks as a single block. A “Play Selection” option lets you select any phrase or block and play it instantly. You can cut, copy, paste, or delete any part of a MIDI or audio track–or double-click on a block to go to another editing screen.

Mixing Consoles
Studio Vision Pro’s mixing and monitoring sections have all the features you would expect in a professional recording package, plus some unique features you won’t find anywhere else. Use the “Build From Selected Tracks” command and you get a console for the audio and MIDI tracks you have selected! You can choose between a narrow-module console, to fit the maximum number of tracks on screen, or a wide-module console with TDM inserts, remote devices, and stereo VU Meters. Just click on the image to the left to see the full wide-module console.
Record Monitor
The Record Monitor window has accurate peak-hold meters with a VU weighting, so it’s easy to set the proper level without guessing. Also displayed are available record time (based upon hard disk space), input select, and audio thru select. Advanced record ing features allow you to Append Record a file or to punch-in to an existing track.

DSP Menu
Take a good look at Studio Vision Pro 3.0’s new DSP Menu. At first glance it may seem familiar, the items at the top–Normalize, Reverse, Invert Phase, Sample Rate Conversion and EQ–are common features of many disk-based recording systems. As you move do wn the menu you’ll notice features you’ve never seen in any digital audio recording or MIDI sequencing package, features which unlock a new universe of musical possibilities. Studio Vision’s on-board DSP functions don’t require any external devices or add -on cards–and they’re “constructive” creating a new file; always retaining your original file.

Adjust Audio Tempo lets you make tempo changes to your digital audio file. Select Tempo Map from the pop-up menu, and the audio will follow the tempo changes of the MIDI file to which it has been mapped–even the most gradual ritard can be easily a ccomplished. Alternately, you can select New Tempo and enter static tempo values; for example a two-bar sampled drum loop can be adjusted to fit the tempo of your tune.

Select Audio-to-MIDI, and Pro 3.0 will open a dialog box which allows you optimize your Audio-to-MIDI conversion. A pop-up template menu lets you set defaults for the entire dialog box based upon the characteristics of the audio e vent you are going to convert. Then Pro 3.0 opens a window which shows both the digital audio and a new MIDI representation (piano roll, notation, strip chart, etc.) of the same file.

You can edit this file using any of the views or tools that you might normally use to edit MIDI sequences! Fix a bad vocal note, create a distinctive vocal harmony line, or change the tempo of a rhythm guitar part. When you’ve finished editing MIDI parame ters, simply choose MIDI-to-Audio and choose which MIDI parameters will be applied to your original audio performance. Click OK and the program will construct a new digital audio file which includes your edits. The possibilities are limited only by your imagination.

Shifting Pitch is a simple musical operation with Studio Vision Pro 3.0. Just select the musical interval and Studio Vision does the rest. There is even a fine-tuning adjustment that lets you enter values in cents.

Using the Time Scale dialog, you can control audio time compression or expansion musically– in bars and beats– or use SMPTE to map start and stop times.

OMS and Galaxy Integration
Bundled with Studio Vision Pro 3.0 are two highly integrated programs that will simplify your life: OMS 2.O, the Open Music System, and Galaxy, The Universal Librarian. OMS 2.0 makes studio setup easy. Step-by-step prompts help you identify, name, and ass ociate your studio gear with icons for quick reference. Once you’re set up, OMS lets you access and organize your studio quickly, without having to remember details such as channel assignments and port numbers.

Additionally, OMS integrates with Galaxy, a program that lets you store your patches, and organize them in banks, bundles, and libraries.

Using OMS’ flexible Name Browser, you can access all of the patches in your Galaxy files by name, number, or keyword–even beyond the “128 limitation” normally imposed by MIDI program changes!

An OMS Movie Player lets you view QuickTime movies while working with your audio/MIDI tracks. Precision timing services give you accurate synchronization.

Studio Vision Pro 3.0 System Requirements

• 1.4 Megabyte Floppy Drive
• Macintosh IIci (minimum), 68040 Power Macintosh (recommended) with System 7.0 or later
• 32 bit addressing
• 12 or more megabytes of RAM
• 18 millisecond or faster hard drive
• Digidesign Hardware* or Yamaha Hardware*
• Apple Sound Manager 3.1*

*3rd PARTY HARDWARE & SOFTWARE GUIDE

Digidesign

• Pro Tools III
• TDM
• Pro Tools II
• Session 8
• Sound Tools II
• Audio Media II
• 888 I/O audio interface
• 882 I/O audio interface
• 442 audio interface
• 882 studio interface

Yamaha

• CBX-D3
• CBX-D5

Apple Sound Manager 3.1, for 16 bit audio

• Power Macintosh — 7100, 8100, 8500, 9500
• PowerBook — 520, 540
• Quadra — 660AV, 840AV

Trademarks Are The Property Of Their Respective Holders

Why Use Studio Vision Pro?
Opcode’s Studio Vision made history in 1990, as the first program to integrate MIDI and audio recording. This latest incarnation affirms that it remains the best. Put simply, no other program offers so much control, over so many facets of music and sound production, and with so much ease, as Studio Vision Pro 3.0.

Music Recording —
Fast Sessions, Seamless Edits, Flawless Performances Studio Vision Pro’s slick, unified interface handles tracking, editing, DSP effects, mixing, and more. Check out remarkable features such as:

• Integrated MIDI and audio — no waiting for sync lock-up!
• Seamlessly pitch correct single notes or passages
• Compile multiple takes into one.
• Convert audio to MIDI (record the sound of a thigh being slapped, and make it a perfectly timed snare drum!).
• Quantize rhythm guitar and other parts.
• Transpose MIDI sequences–and make the audio match
• Create instant harmonies.
• Adjust the tempo of audio tracks to match MIDI tempos, without changing the pitch!
• External time code sync lets you fly tracks off tape into Studio Vision Pro for editing or DSP, and then back onto reel or cassette.

The list goes on, but why keep reading about it? Studio Vision Pro is ready to track when you are–see for yourself exactly what it has contributed to scores of hit records.

Scoring, Composition, Songwriting, & Arranging —
Tap Into Unlimited Creative Potential Everyone in the business of making melodies dreams about the day when what’s heard in the head can instantly become a musical reality. Studio Vision Pro brings that day all that much closer:

• Sing or hum a melody; have Studio Vision Pro play it back as whatever MIDI instrument you choose.
• Supplement MIDI tracks with real instruments or vocals.
• Enhance any audio track with a parallel or harmony MIDI part.
• Scoring to picture? Transfer workprint audio into your session, and you’ll get to compose with dialogue and sound effects in place.
• Capture the workprint’s video as a QuickTime movie (or ask your video editor for a QuickTime cut) — get instant, accurate visual references, without waiting for video decks to shuttle and lock.
• Automatically separate a rap into individual words — then stutter them, overlap them, double them, harmonize them!
• Pitch correct any audio. And when you’re all done, creating a professional multi-part notation score is as simple as opening your session into Opcode’s new Overture program.

Audio Post-Production for Film & Video —
Speak Your Effects to Spot Them and Other Amazing Tricks While many of Hollywood’s leading audio engineers, editors, and sound designers have discovered the power of Studio Vision Pro, Its new capabilities let you go beyond what you would have imagined possible:

• Integration of sample-triggered MIDI events and audio tracks within the same file.
• Cue list-type entry and editing of MIDI events.
• “Electronic Foley” capabilities for spotting MIDI-triggered samples to QuickTime movies or external video.
• Speedy, nondestructive multi-take recording (great for ADR).
• Text-based markers for “informed” autolocating and spotting.
• Watch the picture while you record your voice and say different sound effects, such as “gun shot,” “door squeak,” or “footstep” — and then, incredibly, use Studio Vision Pro to replace your voice automatically with your desired effects! Any way you cut it, Studio Vision Pro means post as you never imagined it.

Multimedia Production —
The Developer’s Dream ToolStudio Vision Pro is ideal for multimedia development, offering:

• Recording, editing, processing and mixing of every audio element, including voiceovers, audio soundtracks, MIDI soundtracks, and sound effects.
• For team-based development, composers can provide completed MIDI or audio files for instant import.
• Mixes can be exported (with or without sample rate conversion) to authoring programs and video editing systems, including the Avid Media Composer and the Data Translations Media 100.
• Accurate synchronization to QuickTime movies. For everything from games, to CD-ROM books, to authored presentations, Studio Vision Pro is your one-stop-audio-shop. Broadcast Production —
  On The Air, On-Time, and On-Track Today’s broadcasting business makes serious demands on your production capabilities, and Studio Vision Pro has the solutions you need:
• Fast, easy, accurate audio waveform editing.
• From mono to 32 simultaneous tracks.
• On-air talent can have instant playback access to thousands of sound effects.
• Use layered tracks and built-in signal processing to create new spots that sound ten times as good, in a tenth the time.
• Forget about carts: Studio Vision Pro stores hundreds of stereo IDs, commercials, PSAs, and other spots on one or more hard drives — in hourly, daily, weekly, or monthly sequences (which can be instantly changed), with lightning-fast playback, and with consistent full CD-quality.
• Add a complete Studio Vision Pro system, including a Mac and hard drive, for the price of an open-reel 2-track.
• Set up near-maintenance-free production studios anywhere you have a desk and a pair of headphones. Bottom line? For on-air, get on-line with Studio Vision Pro.

http://www.oldschooldaw.com/forums/index.php?topic=16.0

http://macos9lives.com/smforum/index.php?topic=278.0

This is the last version of Studio Vision Pro. This is a MIDI sequencing program and also Audio editor because it is the PRO version. You have to install OMS first to make it work.

Install_OMS_2.3.8.sit (2.5 MiB / 2.62 MB)
OMS 2.3.8 Installer

51 / 2017-04-10 / 6b9d397415b7229fe3df3580990c723004c6d8ce

Galaxy_2.5.4.sit (4.84 MiB / 5.08 MB)
Galaxy 2.5.4

51 / 2017-04-10 / aa44efb79be85a9f840d6169609de37e89059a24

Studio_Vision_Pro_4.5.sit (13.04 MiB / 13.68 MB)
Studio Vision 4.5

74 / 2017-04-10 / 4080ee08076160d9d112adf911e00c56c891

another blast from the past now fully functional again
Master Tracks Pro VI
also have working versions of Alchemy & Sound Diver running
have various oldschool samplers for using with them
throwing midi at 7100 from another machine
then sync them using MTC or something
so can SMPTE/MTC sync 8 track R8 or Tascam 488
Opcode Translator Prosync is now operational on 7100/G3

next…

What a fucking pain…
spent all day yesterday cannibalizing 8600av
rebuilding the nubus 7100 G3
can’t get any SCSI CD rom drive working
have an original 1x caddy CD Rom from quadra950
yet that is being used with ASR10r
may need doing floppy zip or ez drive transfers
no clue why it isn’t recognizing the Lacie external CD rom/writer
contemplating manual XLR audio transfers from the 7100
Protools rack to Protools rack
went around in circles yesterday and studio looks like a deathstar trash compactor today
have it 90%+ functional
yet need doing file I/O somhow besides direct audio signal
plus need putting turbosynth on 7100
anyways
cleaning up all the parts strewn ever where
from hybrid hack attack operations on that machine

March 14, 1994: Apple introduces the Power Macintosh 7100, a midrange Mac that will become memorable for two reasons.

The first is that it is among the first Macs to use new PowerPC processors. The second is that it results in Apple getting taken to court by astronomer Carl Sagan — not once but twice.
Power Macintosh 7100: A solid Mac

The Power Macintosh 7100 was one of three Macs introduced in March 1994, with the other two being the lower-end Power Macintosh 6100 and the high-end 8100 model.

The Power Mac 7100’s PowerPC processor ran at 66 MHz (a spec that Apple upgraded to 80 MHz in January 1995). The computer’s hard drive ranged between 250MB and 700MB in size. The Mac also sported Apple’s then-standard NuBus card slots and 72-pin paired RAM slots.

The Mac 7100 came in a slightly modified Macintosh IIvx case. (The IIvx was the first Mac to come in a metal case and feature an internal CD-ROM drive.)

Costing $2,900 to $3,500, the Mac 7100 was a solid piece of hardware that bridged the gap nicely between the low-end consumer 6100 and its higher-end 8100 sibling. It was, for example, perfectly capable of running two monitors. However, it could overheat when performing particularly strenuous tasks like complex rendering of images or videos.

PowerPC
The Mac 7100 compared with the other Power Macintoshes of its day.

Carl Sagan sues Apple over Power Mac 7100 code name
Sagan
Carl Sagan wasn’t on the best terms with Apple in 1994.

Photo: Carl Sagan Planetary Society CC

As many Apple fans will know, the company’s engineers frequently give code names to projects they’re working on, either for secrecy reasons or just for fun. They gave the Power Mac 7100 the code name “Carl Sagan” as a tribute to the famous astronomer.

Unfortunately, the secret in-joke spilled in a 1993 issue of MacWeek that eventually found its way into Sagan’s hands. In a letter to MacWeek, Sagan wrote:

“I have been approached many times over the past two decades by individuals and corporations seeking to use my name and/or likeness for commercial purposes. I have always declined, no matter how lucrative the offer or how important the corporation. My endorsement is not for sale.

For this reason, I was profoundly distressed to see your lead front-page story ‘Trio of Power PC Macs spring toward March release date’ proclaiming Apple’s announcement of a new Mac bearing my name. That this was done without my authorization or knowledge is especially disturbing. Through my attorneys, I have repeatedly requested Apple to make a public clarification that I knew nothing of its intention to capitalize on my reputation in introducing this product, that I derived no benefit, financial or otherwise, from its doing so. Apple has refused. I would appreciate it if you so apprise your readership.”

A new code name: ‘Butt-Head Astronomer’

Forced to change the code name, Apple engineers began calling the project “BHA,” which stood for “Butt-Head Astronomer.”

Sagan sued Apple over the implication that he was a “butt-head.” The judge overseeing the matter made the following statement:

“There can be no question that the use of the figurative term ‘butt-head’ negates the impression that Defendant was seriously implying an assertion of fact. It strains reason to conclude the Defendant was attempting to criticize Plaintiff’s reputation of competency as an astronomer. One does not seriously attack the expertise of a scientist using the undefined phrase ‘butt-head.’”

Still, Apple’s legal team asked the engineers to change the code name once more. They picked “LAW” — standing for “Lawyers Are Wimps.”

Sagan appealed the judge’s decision. Eventually, in late 1995, he reached a settlement with Apple. From that point on, Cupertino appears to have used only benign code names related to activities like skiing.

Getting ancient Digidesign SampleCell working with ProTools on Nubus Mac
why the fuck would eye do that?
hmm where exactly did this sample cell card get used for years making records?
“Chicago Trax”
yo dawg waz dat???!
ended up with it when nubus was decommissioned(eye was given samplecell)
plus bags of ram and other nubus cards including the proto protools system(sound accelerator)
maybe some of you can comprehend why eye would even be obsessing on such a project
turns my Mac 7100(G3 upgraded) machine into visual editor hardware sampler via midi
plus want using it with vintage samplers because nothing modern really compares
yet that machine has no SCSI CDrom & need installing software/extensions
probably need booting up 8600av for using so can make floppies between machines
what a pain jumping through hoops
hmm how the fuck did eye used to do this….
ummm oh yeah
appletalk network & external SCSI raid
looks like time for power up the old 8600av in studio
grabbing “warez” from the Mac Repository eye recently discovered
that place is AWESOME!!!

Wanna help and be part of the MR project? Awesome, because we need a bit of your time!
• Upload missing software files
• Upload missing software screenshots
• Set missing software categories
• Set missing software architecture
• Set any description and compatibility notes you see incorrect or missing!

ATTENTION! We’re looking for a working copy of:
• Every Mac OS 8.0 and 8.1 pre-releases (around 1997)
• Mac OS 8.5f3 Beta (around 1998)